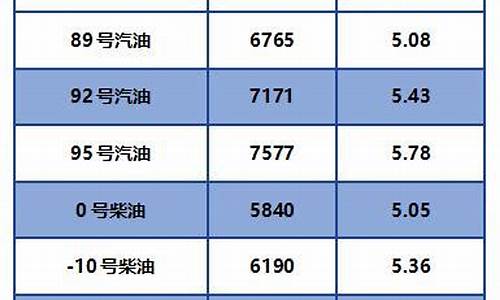
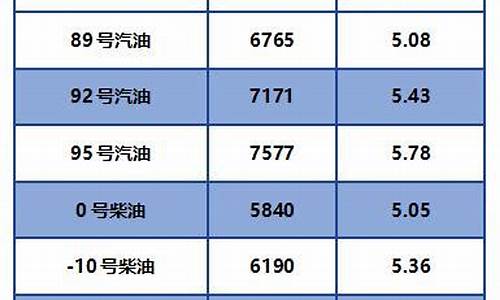
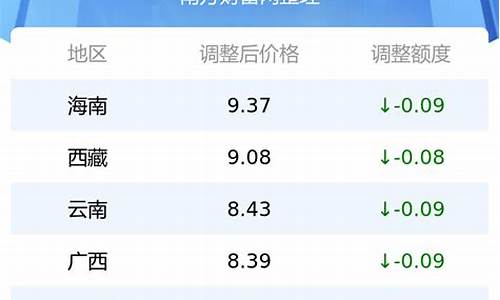
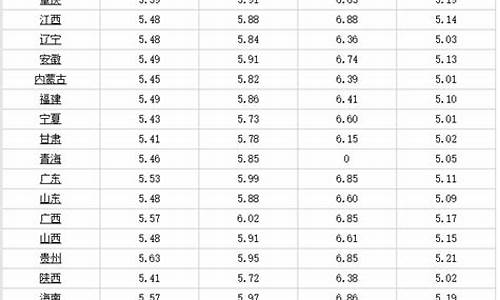
2021年4月24日油价_二o二四年四月30日油价走势

1.请问 2011年5月以后到2012年 哪天登记是好日子？男的：1987年04月10日 女的：1987年02月07日

2.二零二四年三月廿二（2024年4月30日）出生的男宝宝名字

3.初中数学联赛试题提供2006—2009

一般情况下是每隔十九年阴历阳历重合一次，有时也会差一天。

公历：2015年4月18日星期六白羊座

农历：一五年 二月 三十

干支：乙未 庚辰 甲子

公历：2034年4月18日星期二白羊座

农历：三四年 二月 三十

干支：甲寅 戊辰 甲辰

信息来源：华···网

请问 2011年5月以后到2012年 哪天登记是好日子？男的：1987年04月10日 女的：1987年02月07日

女宝宝出生信息

公历生日：2024年4月30日

农历生日：二零二四年?三月廿二

五行旺缺：请对照下方出生时辰星座：金牛座

生肖：属龙

日柱：甲子

命格：正印格

本命佛：千手观音菩萨

今天出生的男孩取名

今日出生喜金起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

华诗(71) 春洋(89) 灵聪(84) 如沛(72) 秀卿(84) 珊静(89) 馨荷(70) 若翠(70) 萱锦(69) 羽春(86) 风笑(71) 如可(90) 惜新(93) 舒金(79) 悦筠(86) 素希(72) 如寒(72) 飞初(89) 书金(93) 彩纯(90) 安倪(85) 洁韶(70) 菁柔(93) 书丝(86) 思曼(68) 盼素(88) 笑荷(81) 聪胜(78) 代翠(89) 蕊柔(75) 晶丝(92) 思海(93) 旋怜(75) 红舒(74) 凤真(87) 凡真(86)

今日出生喜木起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

茜蔓(73) 贤莺(84) 贤欣(89) 琬草(69) 贤梦(90) 艺萌(73) 雪姣(74) 蕊枫(91) 宛雁(81) 幼颖(90) 平若(90) 枫琴(75) 宜菱(70) 迎窍(70) 诗葆(92) 素颂(76) 叶凯(81) 琴柳(91) 宛芙(87) 梦勤(84) 丝苑(87) 贤雁(76) 雪梵(83) 灵巧(93) 欣语(90) 秀兰(76) 蓝艺(85) 娟荣(84) 如颜(70) 苑桃(83) 新卉(86) 彦绮(74) 颖桃(89) 黛君(81) 倩萃(89) 洋柯(69)

今日出生喜水起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

初苗(79) 翠屏(87) 莉美(79) 嘉玛(71) 贤惠(81) 松曼(85) 眉霄(86) 荣妍(68) 凤玫(69) 凤骅(93) 桦澜(77) 觅涵(70) 碧盈(84) 雪寒(86) 逸幂(75) 希霄(87) 碧露(77) 映苗(78) 雨扉(86) 海霞(90) 若妍(89) 觅苗(91) 霞涛(93) 叶彭(73) 水骅(69) 慧沛(91) 宇清(80) 松贝(93) 秀馥(93) 易风(93) 绮清(73) 露泉(82) 凝雯(85) 苇文(77) 娟含(90) 梅熙(73)

今日出生喜火起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

瑞天(70) 纳志(70) 凌晓(71) 定衷(86) 哲庭(86) 昆利(80) 艺腾(81) 滕良(70) 仲焱(68) 瑾隆(86) 霞泰(80) 韬振(93) 狄(86) 红灵(92) 腾智(83) 芬曙(81) 天旻(86) 霄忠(91) 媚振(77) 洋玲(90) 煊多(70) 亘廷(91) 清俊(84) 尔黛(92) 大利(74) 焱中(73) 瑾多(80) 大翎(86) 畅瑾(86) 向(79) 枫腾(93) 滢瑄(93) 昆丽(82) 昆传(84) 朗中(90) 炜俊(85)

今日出生喜土起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

圆艳(86) 幽梵(92) 园姣(79) 初翔(91) 荷忆(74) 宇巧(82) 融萱(77) 华忆(80) 艳如(91) 慕羽(74) 玥玛(86) 咏宇(83) 阿梅(86) 灵怡(75) 圣琳(78) 羽荣(93) 园欢(83) 宛依(76) 飞琬(85) 婉璧(75) 宇桃(83) 碧玥(86) 幼艳(81) 娅菲(93) 双玮(70) 燕忆(77) 娅以(93) 幽瑶(72) 维雅(79) 薇友(76) 娅逸(69) 幽琴(72) 亦娅(78) 勤颐(75) 凡韵(79) 安娅(76)

您还可以点击底部客服给您的宝宝起名，赐子千金不如赐子好名，很多家长都关注了我们，我们会根据宝宝出生年月日，为宝宝起一个带着一生好运的好名字：://.adxqd/qiming/

二零二四年三月廿二（2024年4月30日）出生的男宝宝名字

吉祥温馨提示---您二位的生肖* *年类别： 丁卯

男的：1987 丁卯 年04月10日

女的：1987 丁卯 年02月07日

6月为您二位结婚领证的吉月--极好，下列没有不利您的冲 丁卯 日！

2011年6月份恭候您二位结婚领证的黄道吉日是：

(避开公休日后可以任选)

2011年06月03日 农历05月02日 星期五 冲羊(癸未) 玉堂成日佳日

2011年06月10日 农历05月09日 星期五 冲虎(庚寅)

2011年06月11日 农历05月10日 星期六 冲兔(辛卯)

2011年06月12日 农历05月11日 星期日 冲龙(壬辰)

2011年06月15日 农历05月14日 星期三 冲羊(乙未) 天德危日佳日

2011年06月18日 农历05月17日 星期六 冲狗(戊戍)

2011年06月21日 农历05月20日 星期二 冲牛(辛丑)

祝愿你们美满幸福！

初中数学联赛试题提供2006—2009

男宝宝出生信息

阳历生日：2024年4月30日

阴历生日：二零二四年?三月廿二

五行旺缺：请对照下方出生时辰星座：金牛座

生肖：属龙

日柱：甲子

命格：正印格

本命佛：千手观音菩萨

今天出生的女孩取名

今日出生喜金起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

才少(84) 宗司(81) 西骏(75) 东青(81) 庆仁(70) 杰琒(69) 雄朝(89) 齐纯(70) 兴翱(78) 江昌(75) 锌晨(86) 启任(69) 澄锡(90) 心楚(91) 绍秋(90) 颂琤(77) 世靖(92) 金西(93) 楠笑(91) 纯才(81) 骏星(88) 田心(68) 利锡(82) 茂青(72) 仲仁(93) 桦笑(72) 然庚(74) 杉朝(80) 渝秀(93) 心承(93) 峰佐(69) 刚歆(83) 刚顺(74) 克斯(93) 权瑞(93) 瀚劭(77)

今日出生喜木起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

敬宸(78) 欣佳(93) 道庆(78) 钧栩(84) 润谨(92) 欣颖(71) 启杉(93) 辰谨(79) 云冠(75) 克旭(68) 腾启(82) 靖林(82) 枫驹(71) 楠冠(90) 乔语(94) 润尧(79) 羲桐(80) 贯良(84) 乐歌(91) 郴霖(88) 尧赫(94) 基榕(92) 杉岑(88) 才桦(74) 宁谨(80) 协可(93) 群毅(68) 旭克(77) 旭君(76) 隽格(81) 俊奇(81) 冠勤(74) 虹可(73) 儒元(81) 茂广(72) 冠健(90)

今日出生喜水起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

涛裕(93) 慧鸣(90) 鑫平(84) 飞贤(93) 鸣霖(92) 安白(82) 清豪(84) 飞霏(69) 飒道(93) 霜辰(68) 浩雨(82) 明富(75) 斌义(91) 韩军(79) 帆民(89) 海枫(87) 海峰(80) 震峻(82) 辉风(75) 然渝(68) 子钢(86) 泽瀚(93) 瑄冰(86) 宏伊(86) 狄帆(87) 侨鹏(93) 河明(93) 民百(75) 杰雪(92) 霆奇(93) 钢勰(75) 诚民(68) 平慧(74) 雷飞(92) 弘达(94) 兴寒(83)

今日出生喜火起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

克腾(69) 雄同(75) 骏儋(74) 皓琩(81) 映弢(85) 乐俊(94) 麟晓(71) 驰曦(75) 春德(88) 焕昱(82) 熙易(91) 旻烽(88) 全丹(91) 曦赵(91) 俊哲(89) 传烽(86) 嘉曜(69) 纳昮(94) 卫秦(91) 宁亮(85) 亮廷(92) 烽田(80) 仲驰(69) 轮丰(68) 光烽(72) 夏昆(85) 义滕(94) 连全(94) 路道(86) 中狄(72) 灵立(78) 隆力(91) 韬昮(72) 滕(86) 晟仲(86) 宁映(76)

今日出生喜土起名

起名时选用宝宝喜用的五行，参考下方《各出生时辰五行旺缺对照》

宗威(88) 铭阳(93) 逸亚(73) 亚辰(91) 锦为(90) 平韵(86) 臣岩(76) 钢依(86) 兆以(88) 滨以(81) 森恩(84) 升予(92) 卫圣(86) 有逸(70) 雄忆(72) 民忆(82) 鸿亦(90) 宇佑(94) 晨纬(85) 宥威(76) 坤怡(88) 德峥(92) 东鸥(93) 鹏咏(90) 峻予(92) 腾叶(89) 仲坦(92) 青勋(94) 群唯(85) 波鸥(71) 润勇(79) 广益(68) 洋峥(72) 阳山(72) 秋叶(79) 西为(78)

您还可以点击底部客服给您的宝宝起名，赐子千金不如赐子好名，很多家长都关注了我们，我们会根据宝宝出生年月日，为宝宝起一个带着一生好运的好名字：://.adxqd/qiming/

2008年全国初中数学联赛

2008年4月13日上午8：30—9：30

一、选择题：（本题满分42分，每小题7分）

1、设a 2 + 1 = 3 a，b 2 + 1 = 3 b，且a ≠ b，则代数式 + 的值为（ ）

（A）5 （B）7 （C）9 （D）11

2、如图，设AD，BE，CF为△ABC的三条高，若AB = 6，BC = 5，EF = 3，则线段BE的长为（ ）

（A） （B）4 （C） （D）

3、从分别写有数字1，2，3，4，5的5张卡片中任意取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，则所组成的数是3的倍数的概率是（ ）

（A） （B） （C） （D）

4、在△ABC中，∠ABC = 12°，∠ACB = 132°，BM和CN分别是这两个角的外角平分线，且点M，N分别在直线AC和直线AB上，则（ ）

（A）BM > CN （B）BM = CN （C）BM < CN （D）BM和CN的大小关系不确定

5、现有价格相同的5种不同商品，从今天开始每天分别降价10％或20％，若干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r，则r的最小值为（ ）

（A）( ) 3 （B）( ) 4 （C）( ) 5 （D）

6、已知实数x，y满足( x – ) ( y – ) = 2008，

则3 x 2 – 2 y 2 + 3 x – 3 y – 2007的值为（ ）

（A）– 2008 （B）2008 （C）– 1 （D）1

二、填空题：（本题满分28分，每小题7分）

1、设a = ，则 = 。

2、如图，正方形ABCD的边长为1，M，N为BD所在直线上的两点，且AM = ，∠MAN = 135°，则四边形AMCN的面积为 。

3、已知二次函数y = x 2 + a x + b的图象与x轴的两个交点的横坐标分别为m，n，且| m | + | n | ≤ 1。设满足上述要求的b的最大值和最小值分别为p，q，则| p | + | q | = 。

4、依次将正整数1，2，3，…的平方数排成一串：149162536496481100121144…，排在第1个位置的数字是1，排在第5个位置的数字是6，排在第10个位置的数字是4，排在第2008个位置的数字是 。

答案： B、D、C、B、B、D；– 2、 、 、1。

解答：一、1、由题设条件可知a 2 – 3 a + 1 = 0，b 2 – 3 b + 1 = 0，且a ≠ b，

所以a，b是一元二次方程x 2 – 3 x + 1 = 0的两根，故a + b = 3，a b = 1，

因此 + = = = = 7；

2、因为AD，BE，CF为△ABC的三条高，易知B，C，E，F四点共圆，

于是△AEF∽△ABC，故 = = ，即cos∠BAC = ，所以sin∠BAC = 。

在Rt△ABE中，BE = AB sin∠BAC = 6 × = ；

3、能够组成的两位数有12，13，14，15，21，23，24，25，31，32，34，35，41，42，43，45，51，52，53，54，共20个，其中是3的倍数的数为12，15，21，24，42，45，51，54，共8个，所以所组成的数是3的倍数的概率是 = ；

4、∵∠ABC = 12°，BM为∠ABC的外角平分线，∴∠MBC = ( 180° – 12° ) = 84°，

又∠BCM = 180° –∠ACB = 180° – 132° = 48°，∴∠BCM = 180° – 84° – 48° = 48°，∴BM = BC，又∠ACN = ( 180° –∠ACB ) = ( 180° – 132° ) = 24°，∴∠BNC = 180° –∠ABC –∠BCN = 180° – 12° – (∠ACB +∠CAN ) = 12° =∠ABC，∴CN = CB，因此，BM = BC = CN；

5、容易知道，4天之后就可以出现5种商品的价格互不相同的情况。

设5种商品降价前的价格为a，过了n天，n天后每种商品的价格一定可以

表示为a ? ( 1 – 10% ) k ? ( 1 – 20% ) n – k = a ? ( ) k ? ( ) n – k，其中k为自然数，且0 ≤ k ≤ n，要使r的值最小，五种商品的价格应该分别为：a ? ( ) i ? ( ) n – i，a ? ( ) i + 1 ? ( ) n – i – 1，a ? ( ) i + 2 ? ( ) n – i – 2，a ? ( ) i + 3 ? ( ) n – i – 3，a ? ( ) i + 4 ? ( ) n – i – 4，

其中i为不超过n的自然数，所以r的最小值为 = ( ) 4；

6、∵( x – ) ( y – ) = 2008，∴x – = =

y + ，y – = = x + ，

由以上两式可得x = y， 所以( x – ) 2 = 2008，解得x 2 = 2008，

所以3 x 2 – 2 y 2 + 3 x – 3 y – 2007 = 3 x 2 – 2 x 2 + 3 x – 3 x – 2007 = x 2 – 2007 = 1；

二、1、∵a 2 = ( ) 2 = = 1 – a，∴a 2 + a = 1，∴原式=

= = = – = – ( 1 + a + a 2 ) = – ( 1 + 1 ) = – 2；

2、设BD中点为O，连AO，则AO⊥BD，AO = OB = ，MO = = ，

∴MB = MO – OB = 。又∠ABM =∠NDA = 135°，

∠NAD =∠MAN –∠DAB –∠MAB = 135° – 90° –∠MAB = 45°–∠MAB =∠AMB，

所以△ADN∽△MBA，故 = ，从而DN = ? BA = × 1 = ，根据对称性可知，

四边形AMCN的面积S = 2 S△MAN = 2 × × MN × AO = 2 × × ( + + ) × = ；

3、根据题意，m，n是一元二次方程x 2 + a x + b = 0的两根，所以m + n = – a，m n = b。

∵| m | + | n | ≤ 1，∴| m + n | ≤ | m | + | n | ≤ 1，| m – n | ≤ | m | + | n | ≤ 1。

∵方程x 2 + a x + b = 0的判别式△= a 2 – 4 b ≥ 0，∴b ≤ = ≤ 。

4 b = 4 m n = ( m + n ) 2 – ( m – n ) 2 ≥ ( m + n ) 2 – 1 ≥ – 1，故b ≥ – ，等号当m = – n = 时取得；4 b = 4 m n = ( m + n ) 2 – ( m – n ) 2 ≤ 1 – ( m – n ) 2 ≤ 1，故b ≤ ，等号当m = n = 时取得。所以p = ，q = – ，于是| p | + | q | = ；

4、1 2到3 2，结果都只各占1个数位，共占1 × 3 = 3个数位；4 2到9 2，结果都只各占2个数位，共占2 × 6 = 12个数位；10 2到31 2，结果都只各占3个数位，共占3 × 22 = 66个数位；32 2到99 2，结果都只各占4个数位，共占4 × 68 = 272个数位；100 2到316 2，结果都只各占5个数位，共占5 × 217 = 1085个数位；此时还差2008 – ( 3 + 12 + 66 + 272 + 1085 ) = 570个数位。317 2到411 2，结果都只各占6个数位，共占6 × 95 = 570个数位。所以，排在第2008个位置的数字恰好应该是411 2的个位数字，即为1；

2008年全国初中数学联赛

2008年4月13日上午10：00—11：30

第二试 （A）

一、（本题满分20分）已知a 2 + b 2 = 1，对于满足条件0 ≤ x ≤ 1的一切实数x，不等式a ( 1 – x ) ( 1 – x – a x ) – b x ( b – x – b x ) ≥ 0 （1）恒成立，当乘积a b取最小值时，求a，b的值。

解：整理不等式（1）并将a 2 + b 2 = 1代入，得( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a ≥ 0 （2），

在（2）中，令x = 0，得a ≥ 0；令x = 1，得b ≥ 0。易知1 + a + b > 0，0 < < 1，

故二次函数y = ( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间。由题设知，不等式（2）对于满足条件0 ≤ x ≤ 1的一切实数x恒成立，所以它的判别式△= ( 2 a + 1 ) 2 – 4 a ( 1 + a + b ) ≤ 0，即a b ≥ 。由方程组 （3）

消去b，得16 a 4 – 16 a 2 + 1 = 0，所以a 2 = 或a 2 = 。又因为a ≥ 0，

所以a 1 = 或a 2 = ，于是b 1 = 或b 2 = 。所以a b的最小值为 ，此时a，b的值分别为a = ，b = 和a = ，b = 。

二、（本题满分25分）如图，圆O与圆D相交于A，B两点，BC为圆D的切线，点C在圆O上，且AB = BC。

（1）证明：点O在圆D的圆周上；

（2）设△ABC的面积为S，求圆D的的半径r的最小值。

解：（1）连OA，OB，OC，AC，因为O为圆心，AB = BC，所以△OBA∽△OBC，从而∠OBA =∠OBC，因为OD⊥AB，DB⊥BC，所以∠DOB = 90° –∠OBA = 90° –∠OBC =∠DBO，所以DB = DO，因此点O在圆D的圆周上；

（2）设圆O的半径为a，BO的延长线交AC于点E，易知BE⊥AC。设AC = 2 y（0 < y ≤ a），OE = x，AB = l，则a 2 = x 2 + y 2，S = y ( a + x )，

l 2 = y 2 + ( a + x ) 2 = y 2 + a 2 + 2 a x + x 2 = 2 a 2 + 2 a x = 2 a ( a + x ) = 。

因为∠ABC = 2∠OBA = 2∠OAB =∠BDO，AB = BC，DB = DO，所以△BDO∽△ABC，

所以 = ，即 = ，故r = ，所以r 2 = = ? = ? ( ) 3 ≥ ，即r ≥ ，其中等号当a = y时成立，这时AC是圆O的直径.所以圆D的的半径r的最小值为 。

三、（本题满分25分）设a为质数，b为正整数，且9 ( 2 a + b ) 2 = 509 ( 4 a + 511 b ) （1）

求a，b的值。

解：（1）式即( ) 2 = ，设m = ，n = ，则n = m 2，

b = = （2），故3 n – 511 m + 6 a = 0，所以3 m 2 – 511 m + 6 a = 0 （3），由（1）式可知，( 2 a + b ) 2能被质数509整除，于是2 a + b能被509整除，故m为整数，

即关于m的一元二次方程（3）有整数根，所以它的判别式△= 511 2 – 72 a为完全平方数。

不妨设△= 511 2 – 72 a = t 2（ 为自然数），则72 a = 511 2 – t 2 = ( 511 + t ) ( 511 – t )，

由于511 + t和511 – t的奇偶性相同，且511 + t ≥ 511，所以只可能有以下几种情况：

① ，② ，③ ，④ ，两式相加分别得

36 a + 2 = 1022，18 a + 4 = 1022，12 a + 6 = 1022，6 a + 12 = 1022，均没有整数解；

⑤ ，⑥ ，两式相加分别得4 a + 18 = 1022，解得a = 251；

2 a + 36 = 1022，解得a = 493，而493 = 17 × 29不是质数，故舍去。综合可知a = 251。

此时方程（3）的解为m = 3或m = （舍去）。

把a = 251，m = 3代入（2）式，得b = = 7。

第二试 （B）

一、（本题满分20分）已知a 2 + b 2 = 1，对于满足条件x + y = 1，x y ≥ 0的一切实数对( x，y )，不等式a y 2 – x y + b x 2 ≥ 0 （1）恒成立，当乘积a b取最小值时，求a，b的值。

解：由x + y = 1，x y ≥ 0可知0 ≤ x ≤ 1，0 ≤ y ≤ 1。在（1）式中，令x = 0，y = 1，得a ≥ 0；令x = 1，y = 0，得b ≥ 0。将y = 1 – x代入（1）式，得a ( 1 – x ) 2 – x ( 1 – x ) + b x 2 ≥ 0，

即( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a ≥ 0 （2），易知1 + a + b > 0，0 < < 1，

故二次函数y = ( 1 + a + b ) x 2 – ( 2 a + 1 ) x + a的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间。由题设知，不等式（2）对于满足条件0 ≤ x ≤ 1的一切实数x恒成立，

所以它的判别式△= ( 2 a + 1 ) 2 – 4 a ( 1 + a + b ) ≤ 0，即a b ≥ 。由方程组 （3）消去b，得16 a 4 – 16 a 2 + 1 = 0，所以a 2 = 或a 2 = 。又因为a ≥ 0，

所以a 1 = 或a 2 = ，于是b 1 = 或b 2 = 。所以a b的最小值为 ，此时a，b的值分别为a = ，b = 和a = ，b = 。

二、（本题满分25分）题目和解答与（A）卷第二题相同。

三、（本题满分25分）题目和解答与（A）卷第三题相同。

第二试 （C）

一、（本题满分25分）题目和解答与（B）卷第一题相同。

二、（本题满分25分）题目和解答与（A）卷第二题相同。

三、（本题满分25分）设a为质数，b，c为正整数，且满足 ，求a ( b + c )的值。

解：（1）式即( ) 2 = ，设m = ，n = ，则2 b – c = = （3），故3 n – 511 m + 6 a = 0，又n = m 2，

所以3 m 2 – 511 m + 6 a = 0 （4），由（1）式可知，( 2 a + 2 b – c ) 2能被509整除，

而509是质数，于是2 a + 2 b – c能被509整除，故m为整数，

即关于m的一元二次方程（4）有整数根，所以它的判别式△= 511 2 – 72 a为完全平方数。

不妨设△= 511 2 – 72 a = t 2（ 为自然数），则72 a = 511 2 – t 2 = ( 511 + t ) ( 511 – t )，

由于511 + t和511 – t的奇偶性相同，且511 + t ≥ 511，所以只可能有以下几种情况：

① ，② ，③ ，④ ，两式相加分别得

36 a + 2 = 1022，18 a + 4 = 1022，12 a + 6 = 1022，6 a + 12 = 1022，均没有整数解；

⑤ ，⑥ ，两式相加分别得4 a + 18 = 1022，解得a = 251；

2 a + 36 = 1022，解得a = 493，而493 = 17 × 29不是质数，故舍去。综合可知a = 251。

此时方程（3）的解为m = 3或m = （舍去）。

把a = 251，m = 3代入（3）式，得2 b – c = = 7，即c = 2 b – 7，代入（2）式得b – ( 2 b – 7 ) = 2，所以b = 5，c = 3，因此a ( b + c ) = 251 × ( 5 + 3 ) = 2008。